Quantum Jewels And Hypercubes: The Wild Shapes Of Hyperdimensional Geometry [PICTURES]

If you can ever peer beyond three dimensions, you will be able to see wondrous things: hyperdimensional jewels; shapes made of cubes and spheres arranged in mind-boggling formations. These beautiful geometric specimens are literally out of this world -- which makes it all the more amazing that mathematicians can describe them at all.

Amplituhedron: the quantum jewel

Theoretical physicists don’t usually stumble across beautiful jewels in their line of work, but Harvard physicist Jacob Bourjaily and colleagues recently turned up the mathematical equivalent of a 24-karat. They’ve come up with the model of a strange, many-faceted object that also turns out to be a great way to simplify the math in calculations of subatomic particle interactions.

“Interactions that were previously calculated with mathematical formulas thousands of terms long can now be described by computing the volume of the corresponding jewel-like ‘amplituhedron,’ which yields an equivalent one-term expression,” Natalie Wolchover explains in an extremely thorough write-up for Quanta magazine.

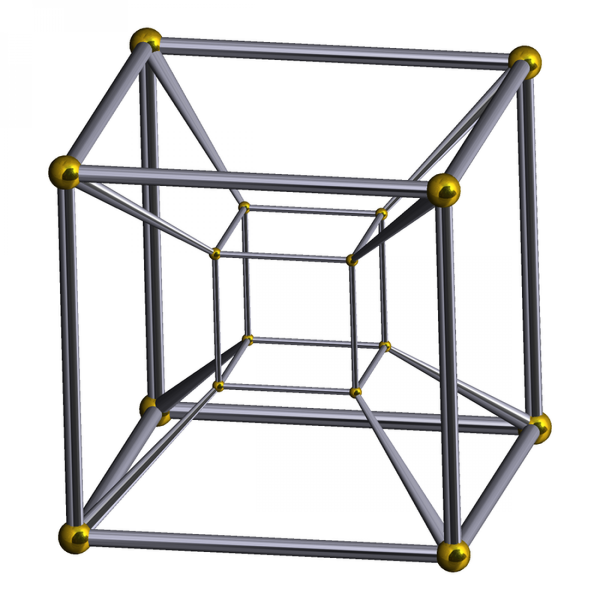
Tesser? I ‘ardly know er!

You might be familiar with the “tesseract” as the glowing blue MacGuffin in The Avengers, or as the secret to faster-than-light travel in Madeleine L’Engle’s novel “A Wrinkle In Time.” But, in reality, the tesseract is just the next step in the evolution of the square; the fourth-dimensional version of a cube. (The image above, created by Robert Webb using his Stella software, represents a tesseract using what's called a Schlegel diagram, which attempts to approximate the twisted physics at play.)

Trying to visualize fourth-dimensional shapes with our three-dimensional mindset is tricky, as author Edwin Abbott illustrated in his novella “Flatland,” where a square comes to terms with knowledge of a fabled third dimension. We perceive our 3-D world through carefully shaded 2-dimensional representations. Now imagine being a 2-dimensional person -- everything around you would be lines, but you would still be able to derive meaning from them. Just as we can look at a flat picture of a cube and infer “cube” without seeing all of the sides at once, a Flatlander can look at a shaded line segment and infer “square” or “triangle.”

Similarly, a resident of the fourth dimension would easily look at a tesseract and see a 3-dimensional representation. But truly grasping this way of seeing things would be as radically jarring to us as it would be to take a Flatlander off of his plane.

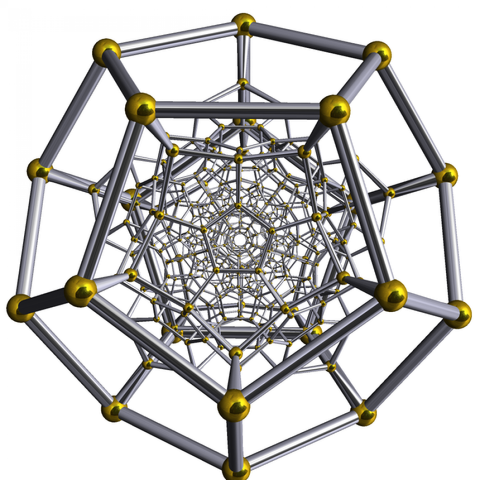
Dodecaplex, aka: the Portal to Insanity

When you stare down the spiraling honeycombed maw of the dodecaplex, you can’t help but think of H.P. Lovecraft’s yarns about cities built on non-Euclidean geometry, populated by the unceasing shrieks of the insane habitants therein. Also known as the hyperdodecahedron, the 120-cell, or the hecatonicosachoron (even more Lovecraftian), the dodecaplex is made up of 120 12-sided polyhedra, resulting in a four-dimensional shape with 1,200 edges, 600 vertices, and 720 pentagonal facets.

Did We All Come From the Fourth Dimension?

There are oodles of other geometric oddities that mathematicians have described: Clifford toruses, n-spheres, duocylinders. Although these extra-dimensional objects might seem foreign, there is at least one theory that says that everything -- humans, geckos, the Earth, Alpha Centauri -- originated from a black hole with four spatial dimensions. Our universe as we know it is just an expanding 3-D bubble surrounding the black hole’s event horizon, Canadian physicists wrote in a paper published on arXiv.org before publication in a peer-reviewed journal.

Such an origin story might explain some of the oddities of our universe: how uniform it is in all directions, and how it has an almost completely uniform temperature, even though “there does not seem to have been enough time since the birth of the cosmos for it to have reached temperature equilibrium,” according to Nature.

So, do not fear the tesseract, the amplituhedron or any other strange fourth-dimensional geometric figures you may encounter in your life: They’re not so alien, after all.